Оформляем условие задачи в виде таблицы:
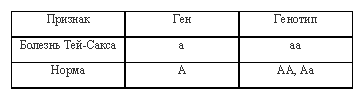
Производим математическую запись закона Харди-Вайнберга p + q = 1, p2 + 2pq + q2 = 1.
p - частота встречаемости гена A;
q - частота встречаемости гена a;
p2 - частота встречаемости доминантных гомозигот (АА);
2pq - частота встречаемости гетерозигот (Aa);
q2 - частота встречаемости рецессивных гомозигот (aa).
Из условия задачи, согласно формуле Харди-Вайнберга, нам известна частота встречаемости больных детей (aa), т.е. q2 = 1/5000.
Ген, вызывающий данное заболевание, перейдёт к следующему поколению только от гетерозиготных родителей, поэтому необходимо найти частоту встречаемости гетерозигот (Aa), т.е. 2pq.
q = 1/71 = 0,014; p =1 - q = 1 - 0.014 = 0,986; 2pq = 2(0,986 * 0,014) = 0,028.
Определяем концентрацию гена в следующем поколении. Он будет в 50% гамет у гетерозигот, его концентрация в генофонде составляет около 0,014. Вероятность рождения больных детей q2 = 0,000196, или 0,000196/0,0002 = 0,98, т. е. 0,98 на 5000 населения. Таким образом, концентрация патологического гена и частота этого заболевания в следующем поколении данной популяции практически не изменится (есть незначительное уменьшение).
Ответ: Концентрация патологического гена и частота этого заболевания в следующем поколении данной популяции практически не изменится (по условию задачи — 1 : 5000, а по расчёту — 0,98 : 5000).