Решение. Построим отрезок АВ, равный данной стороне (рис.202), и проведем прямую а, параллельную прямой АВ и находящуюся от нее на расстоянии,
равном данной высоте (см. задачу 293). За- С а
тем проведем прямую Ь, параллельную АВ и равноудаленную от прямых АВ и а. Далее построим окружность с центром А, радиус которой равен данной медиане, и отметим точку М пересечения этой окружности с прямой Ъ. Наконец, проведем прямую ВЫ до пересечения с прямой а в точке С. Треугольник ABC — искомый.
В самом деле, проведем из точек В и С перпендикуляры ВН\ и СВ.2 к прямой Ь и рассмотрим прямоугольные треугольники ВМН\ и СМН<}. Углы М этих треугольников равны как вертикальные углы, поэтому их углы В и С также равны. Катеты ВН\ и СН^ этих треугольников равны по построению. Следовательно, рассматриваемые треугольники равны по первому признаку равенства треугольников, а значит, ВЫ = МС, т. е. отрезок AM — медиана треугольника ABC.
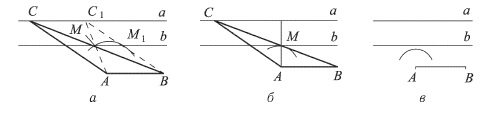
Из построения ясно, что задача может иметь два решения (рис.203, а), одно решение (рис.203, б) или не иметь решения (рис. 203, в).