Так как мы наблюдаем затмения, Земля находится вблизи плоскости орбит двух компонент двойной системы и вблизи плоскости аккреционного диска. Размеры белого карлика и толщина аккреционного диска много меньше размеров гиганта, и падение блеска может вызвать только затмение карлика гигантом. Раз при этом суммарный блеск системы уменьшается на 0.1m, значит светимость белого карлика примерно в 10 раз меньше светимости звезды-гиганта. Зная период обращения T (45.5 суток или 1/8 года) и относительную скорость звезд v (120
км/c), мы получаем расстояние между звездами:
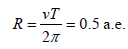
По III обобщенному закону Кеплера получаем, что суммарная масса системы составляет 8 масс Солнца. При этом амплитуда изменения скорости у белого карлика в 7 раз больше, чем у гиганта, следовательно, масса гиганта – 7 масс Солнца, масса карлика – 1 масса Солнца. Во время затмения мы видим только звезду-гигант, ее блеск m на нашем небе равен 4.7m, из измерений параллакса расстояние до нее r = 100 пк. Следовательно, абсолютная звездная величина гиганта равна
m0 = m + 5 − 5lg r = −0.3,
то есть светимость гиганта в 100 раз больше солнечной. Светимость белого карлика I получается равной 10 светимостям Солнца, т.е. 3.88∙10^27 Вт.
Для оценки темпа аккреции примем, что вся кинетическая энергия падающего на белый карлик вещества за период времени Δt переходит в излучение. Эта же величина равна потенциальной энергии упавшего вещества со знаком минус:
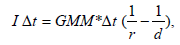
где M и r – масса и радиус белого карлика, d – расстояние от белого карлика до точки либрации, с которой начинается аккреция, M* – темп аккреции. Расстояние d, по порядку величины равное расстоянию между звездами R, значительно больше радиуса белого карлика, и потенциальной энергией вещества в точке либрации можно пренебречь, исключая слагаемое (1/d) в последней формуле. Подставляя далее численные значения, получаем M* = 1.9∙10^14 кг/c или 3∙10–9 масс Солнца в год.