При покрытии далекой звезды Луной область видимости этого явления (назовем ее тенью) движется в пространстве со скоростью, равной скорости орбитального движения Луны, которая минимальна, когда Луна достигает точки апогея своей орбиты. Величину скорости Луны в апогее можно получить из формулы, вытекающей из II закона Кеплера с учетом малости эксцентриситета ее орбиты:
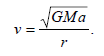
Здесь M - масса Земли, a - большая полуось орбиты Луны, r - расстояние от Земли в апогее. Подставляя численные значения, получаем значение минимальной скорости Луны: 0.962 км/с. Однако нужно еще учесть, что Земля также вращается вокруг своей оси с периодом около 23 часа 56 минут, и точка, находящаяся на экваторе Земли, движется со скоростью 0.465 км/с. Если эти две скорости окажутся сонаправленными, то скорость лунной тени относительно наблюдателя может уменьшиться до 0.497 км/c. Звезда находится от нас несравнимо дальше, чем Луна, и выглядит точкой, а диаметр тени равен диаметру Луны (3476 км). Следовательно, максимальная продолжительность покрытия звезды Луной составит около 1 часа и 56.5 минут